กราฟของฟังก์ชันตรีโกณมิติ
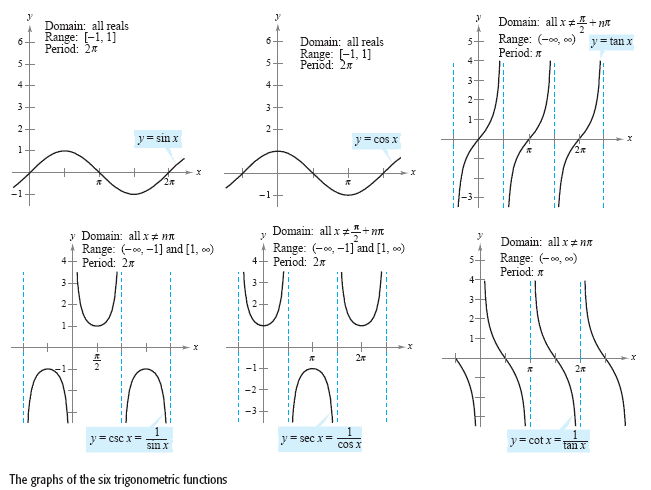
ฟังก์ชันตรีโกณมิติ ทุกฟังก์ชัน เป็นฟังก์ชันที่เป็นคาบ (Periodic Function)
กล่าวคือ สามารถแบ่งแกน x ออกเป็นช่วงย่อย (Subinterval) โดยที่ความยาวแต่ละช่วงย่อยเท่ากัน
และกราฟในแต่ละช่วงย่อยมีลักษณะเหมือนกัน ความยาวของช่วงย่อยที่สั้นที่สุดมีสมบัติดังกล่าวเรียกว่า คาบ (Period)
จากรูปข้างต้น จะเห็นได้ว่า
- คาบของกราฟ y = sinx และ y = cosx เท่ากับ 2π
- คาบของกราฟ y = cosecx และ y = secx เท่ากับ 2π
- คาบของกราฟ y = tanx และ y = cotx เท่ากับ π
สำหรับฟังก์ชันที่เป็นคาบซึ่งมีค่าสูงสุดและค่าต่ำสุด
เราจะเรียกว่าที่เท่ากับครึ่งหนึ่งของค่าสูงสุดลบด้วยค่าต่ำสุดของฟังก์ชันนี้ว่า แอมพลิจูด (Amplitude)
- ฟังก์ชัน y = sinx และ y = cosx มีแอมพลิจูดเป็น 1 เท่ากัน
ฟังก์ชันตรีโกณมิติของผลบวกและผลต่างของจำนวนจริงหรือมุม
การคำนวนค่าฟังก์ชันตรีโกณมิติ อาจเกี่ยวข้องกับมุมที่อยู่ในรูปของผลบวกหรือผลลบ
สูตรที่สำคัญ มีดังนี้
ตัวผกผันของฟังก์ชันตรีโกณมิติ
ฟังก์ชันตรีโกณมิติทั้งหกฟังก์ชัน (เช่น y = sinx) สามารถหาอินเวอร์สได้โดยสลับที่ระหว่างโดเมนและเรนจ์ตามปรกติ (กลายเป็น x = siny)
แต่อินเวอร์สที่ได้เหล่านี้จะไม่เป็นฟังก์ชัน เพราะค่า x แต่ละค่านั้น ให้ค่า y ได้หลายค่าไม่มีที่สิ้นสุด
ดังนั้นหากจะกำหนดอินเวิร์สของฟังก์ชันตรีโกณมิติให้เป็นฟังก์ชันด้วย ก็จำเป็นต้องจำกัดข่วงของเรนจ์ด้วย
นั่นหมายถึง ความหมายของ x = siny และความหมายของ y = arcsinx ไม่เท่ากัน เนื่องจากเรนจ์ไม่เท่ากัน
เราเรียกฟังก์ชันผกผันของตรีโกณมิติโดยใช้คำว่า arc นำหน้า เช่น arcsin arccos arctan เป็นต้น
เอกลักษณ์หนึ่งที่มีประโยชน์ในเรื่องฟังก์ชันตรีโกณมิติผกผัน คือ
ซึ่งเอกลักษณ์นี้สามาถใช้ได้เมื่อ arctanx +arctany ยังอยู่ในช่วง (-π/2,π/2) เท่านั้น
เอกลักษณ์และสมการตรีโกณมิติ
เอกลักษณ์ตรีโกณมิติ คือการเท่ากันของฟังก์ชันตรีโกณมิติที่ต่างกัน และเป็นจริงสำหรับทุก ๆ ค่าของขนาดของมุม
เมื่อกำหนด A เป็นขนาดของมุมใดๆ (0 ≤ A ≤ 2π) จะได้
เมื่อกำหนด x และ y เป็นขนาดของมุมใดๆ (0 ≤ x ≤ 2π , 0 ≤ y ≤ 2π) จะได้
π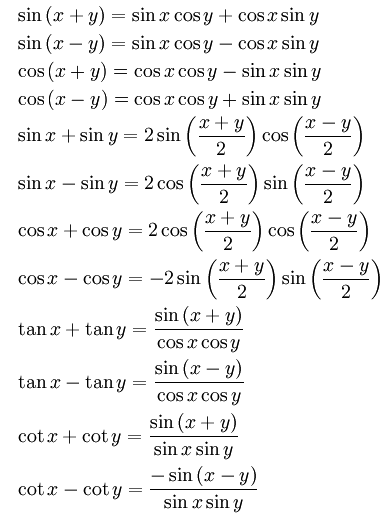
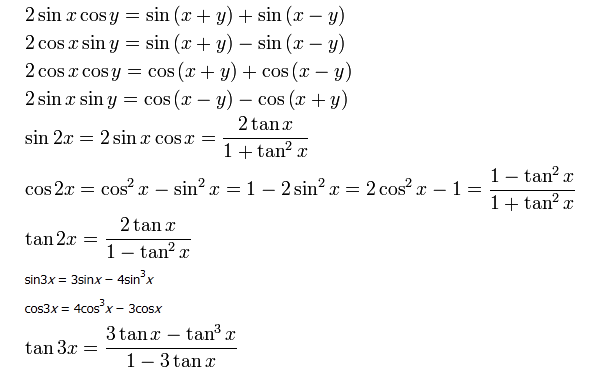
กฎของโคไซน์ และไซน์
กฎของโคไซน์ ในรูปสามเหลี่ยม ABC ใดๆ ถ้า a,b และ cเป็นความยาวของด้านตรงข้ามมุม A,B และ C ตามลำดับ จะได้
a2 = b2 + c2 - 2bc cosA
b2 = c2 + a2 - 2ca cosB
c2 = a2 + b2 - 2ab cosC
กฎของไซน์ ในรูปสามเหลี่ยม ABC ใดๆ ถ้า a,b และ c เป็นความยาวของด้านตรงข้ามมุม A,B และ C ตามลำดับ จะได้
การหาระยะทางและความสูง
ในการวัดระยะทางและความสูงของสิ่งใดก็ตาม บางครั้งจะใช้เครื่องมือสำหรับวัดมาใช้ในการวัดโดยตรงไม่ได้
เช่น การวัดสถานที่สองแห่งที่มีสิ่งกีดขวางกั้นตรงกลาง หรือการวัดความสูงของภูเขา เป็นต้น
เราสามารถนำความรู้ในเรื่องฟังก์ชันตรีโกณมิติ มาประยุกต์ใช้ในการคำนวณได้ อันได้แก่
- มุมก้ม (Angel of Depression) คือมุมที่วังลงไปจากแนวราบ (ระดับสายตา)
- และมุมเงย (Angle of Elevation)คือมุมที่วัดขึ้นจากแนวราบ
- รวมถึงการใช้กฎของไซน์และโคไซน์มาช่วยในการคำนวณ

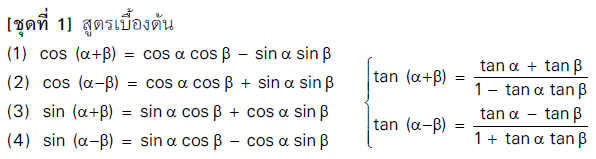



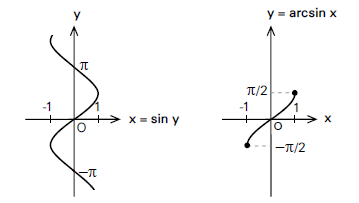
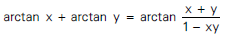
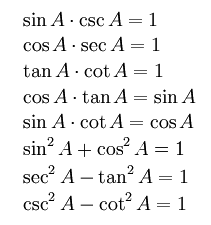
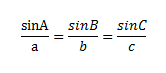
ไม่มีความคิดเห็น:
แสดงความคิดเห็น